Friction and the inclined plane

Objective
To measure the coefficient of friction for several combinations of materials, making use of an inclined plane
Apparatus
- Inclined plane
- Wooden block
- Small cart with wheels
- Weight hanger
- Set of slotted weights
- Clock timer
- Meter stick
Theory
Discussion of friction, and problems about motion on an inclined plane, will be found in any general physics textbook. The basic relation for friction is:

Maximum Force Due to Static Friction
The maximum static friction force is:
fs(max) = μs · N
Force Due to Kinetic Friction
The kinetic friction force is:
Fk = μk · N
Where μs and μk are proportionality constants, called respectively the coefficient of static friction and the coefficient of kinetic friction.
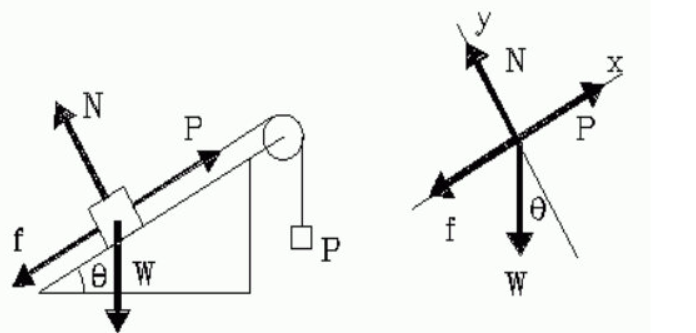
Following the usual notation, the forces acting on a body on an inclined plane are shown in Figure 1. W is the weight of the body (W = m·g), N is the normal force exerted by the plane, f is the frictional force, and P is the applied force when a string is attached to pull the body up the plane.
Generally, this situation is analyzed by resolving the forces into components parallel and perpendicular to the plane, as shown in Figure 2. The components of the weight are:
Wx = W · sinθ
Wy = W · cosθ
Procedure
1-Starting friction on level plane. Lay the wooden block on the plane with its large face down. Apply a force, P, to it by means of a string running over a pulley to a weight hanger. Add weights to the hanger until the block begins to move. In this way determine the approximate value of starting friction. Determine the value more accurately by starting just below this value and adding weight in very small increments. The error may be estimated by noting the smallest additional weight which produces motion. Place 100 grams and 200 grams on the block and repeat
| Masses in gram | W | P[(masses of hunger+ masses we add on hunger )g] | |
|---|---|---|---|
| Mass of block | |||
| Mass of block + 100 | |||
| Mass of block +200 |
2- Sliding friction on level plane. With weight on the block as procedure 1, give the block a push to overcome starting friction and remove weights from hanger until the block slides with nearly constant velocity. There will be quite a lot of uncertainty in determining whether the velocity is constant, so take some care in doing this. Determine carefully the value of the uncertainty in P due to this cause. In some cases it may be necessary to clean the plane with detergent. Do not touch the plane with your hands, for body oil will cause slick spots.
| Masses in gram | W | P[(masses of hunger+ masses we add on hunger )g] | |
|---|---|---|---|
| Mass of block | |||
| Mass of block + 100 | |||
| Mass of block +200 |
Data Analysis
Theory predicts that each coefficient of friction should be constant. Your experimental values may show quite a bit of variation, however. Is this variation due to random error, or is there a residual discrepancy due to systematic error? To answer this question, you must do an error analysis. The contribution of random error is easily calculable from the error in your data by standard error propagation formulae. The equation used was
μ=p-W · sinθ/W · cosθ
The dominant source of error in this equation will probably be the error involved in taking the difference: P – Wsinθ .Verify this with your own error analysis. Compare your calculated probable error in with the average deviation of your experimental values of If the average deviation is greater than the probable error, you probably have a systematic error present. Inspect the variation in in your data. Is dependent on any other data quantity? If so, which one? Try graphing this dependence, indicating the probable error in each value of with an error flag. Is this dependence of any form? Can you suggest any physical reason for such dependence?
Questions
- 1. Would the coefficient of friction of a 3-wheeled car be less than that of a 4 wheeled car, assuming the cars weighed the same, and the wheels were the same? Calculate the ratio of the values of friction coefficient in the two cases.
- 2. Consider the pulley at the top of the plane. How does the friction in the pulley depend on the tension in the string and the angle of the plane? State your assumptions clearly, and derive the equation for the pulley friction.
- 3. The angle of uniform slip is that angle of the plane which causes the free block to slide down the plane with constant velocity. Show that this angle is given by
tanθ=μk
Where μk k is the coefficient of kinetic friction






